6
dec
Möjliga och omöjliga trianglar – att öppna upp för algebraiska resonemang
Dagens nätverkstid ägnades bland annat åt hur olika problemformuleringar kan stimulera till algebraiska resonemang. Exempelvis diskuterades hur följande uppgift skulle kunna fungera just för detta.
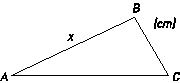
I triangeln nedan är sidan BC 2 cm kortare än sidan AB.
Sidan AC är dubbelt så lång som sidan AB.
Motivera varför triangeln är omöjlig.
Vidare ägnades eftermiddagen åt diskussioner och omformulering av ramprojektets lärandeobjekt: Att utveckla förmågan att kunna resonera kring algebraiska uttryck utan att bestämma värdet på ingående variabler. Med utgångspunkt i tidigare forskning inom området samt i de svårigheter som urskilts i för-förtestet identifierades följande möjliga kritiska aspekter:
- Att urskilja att värdet är principiellt
- Att urskilja det relationella mellan uttryck
- Att urskilja variablers funktion
- Att urskilja vad variabeln representerar i ett uttryck
- Att urskilja variablers inbördes relation, så att de är matematiskt korrekta
- Att urskilja vad siffran representerar i ett uttryck
Med utgångspunkt i ovanstående möjliga kritiska aspekter fastställdes ett förtest. Vi ser fram emot genomförande och analys av förtestet, för att sedan kunna planera för en första forskningslektion.
/Anna-Karin, Jenny, Sanna och Verner




0 kommentarer